FIFO, LIFO Considered Harmful
2017-09-24 - By Robert Elder
The Formal Definition of Stacks and Queues
- A stack is LIFO.
- A queue is FIFO.
Those definitions have always bothered me, and I think I've finally articulated why. To explain myself, I'll start with a typical model of stacks and queues that are presented in CS classes:
Stack (LIFO)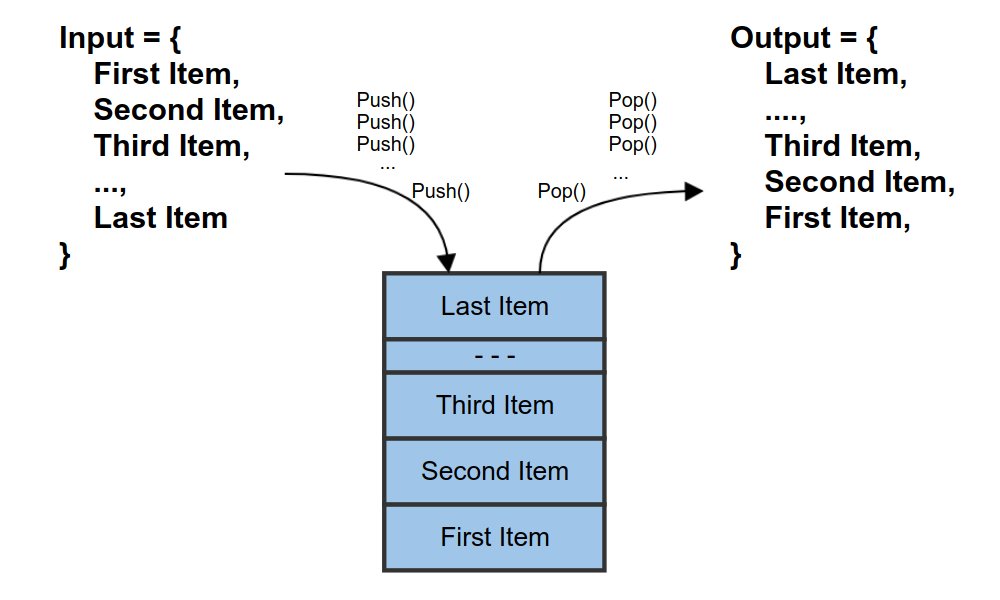 |
Queue (FIFO)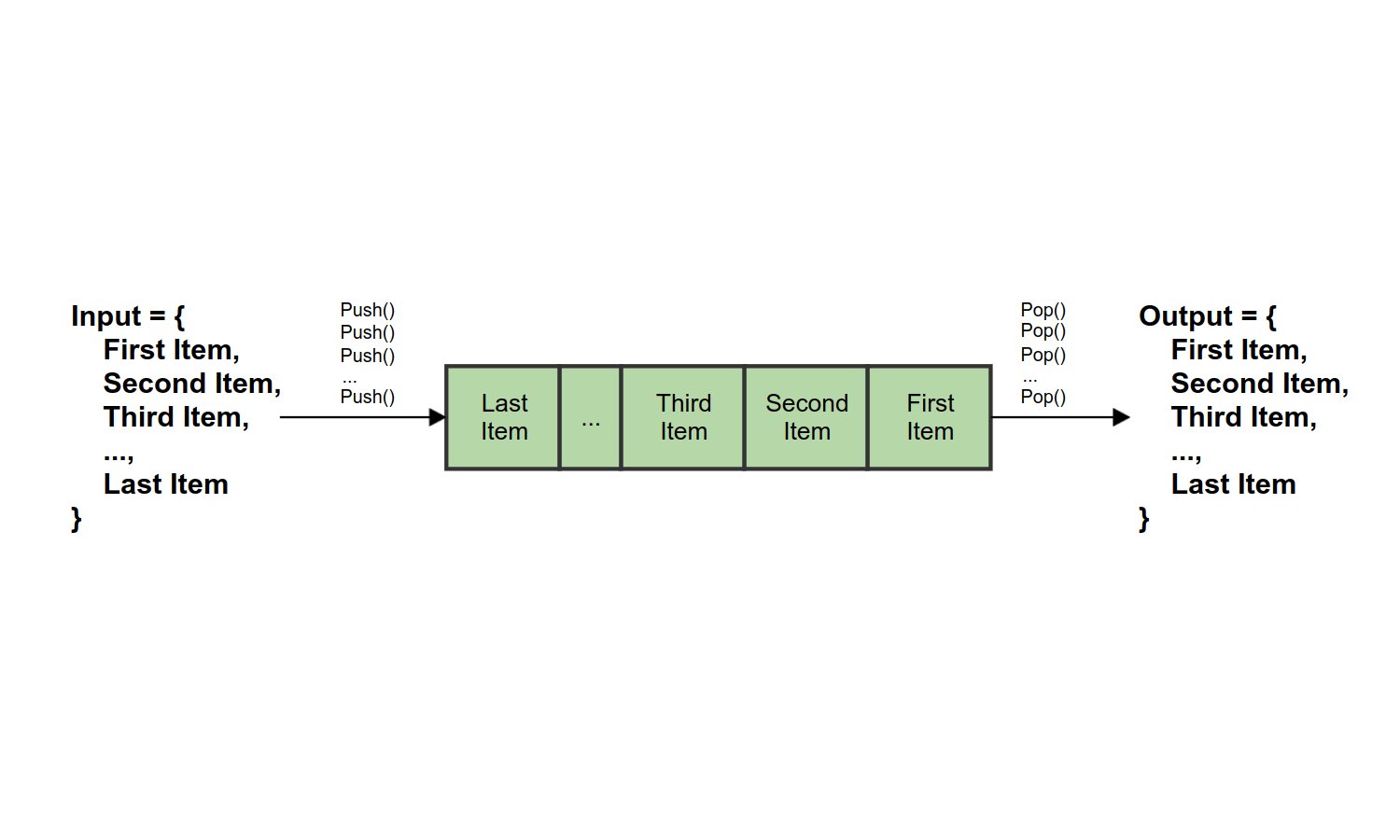 |
This shows the typical 'Last In First Out' (LIFO) and 'First In First Out' (FIFO) model of stacks and queues.
The problem comes about when you consider how mutually exclusive these definitions are. The whole point of making these two definitions is to emphasize that the behaviour of a stack is different from a queue. But are there cases where a stack can exhibit FIFO behaviour, or a queue exhibit LIFO behaviour? The answer is yes: For stacks, this occurs when the sequence of items to be added and then removed is only of size one. For queues, the case is quite similar, but with an added restriction that the queue must be empty before the insertion (although this depends on your definition of 'first' discussed later). In both cases, we can say this happens when the first item is equal to the last item:
Stack (LIFO and FIFO)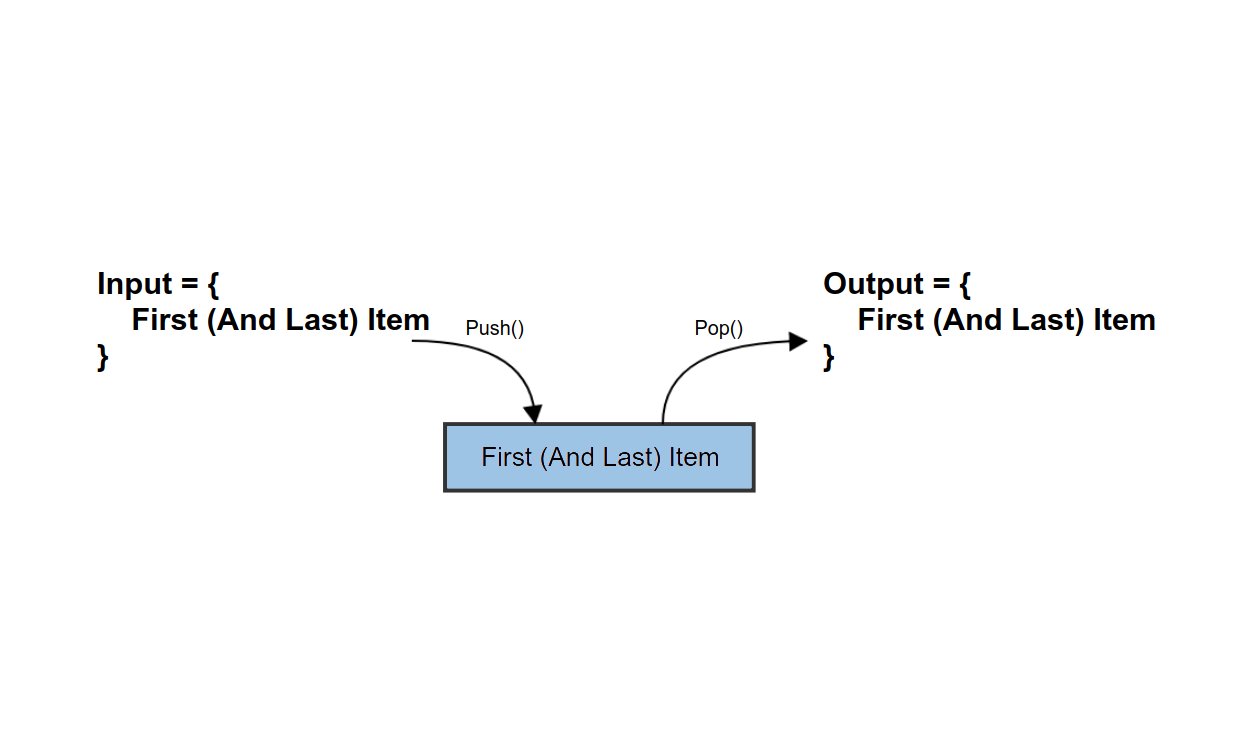 |
Queue (FIFO and LIFO)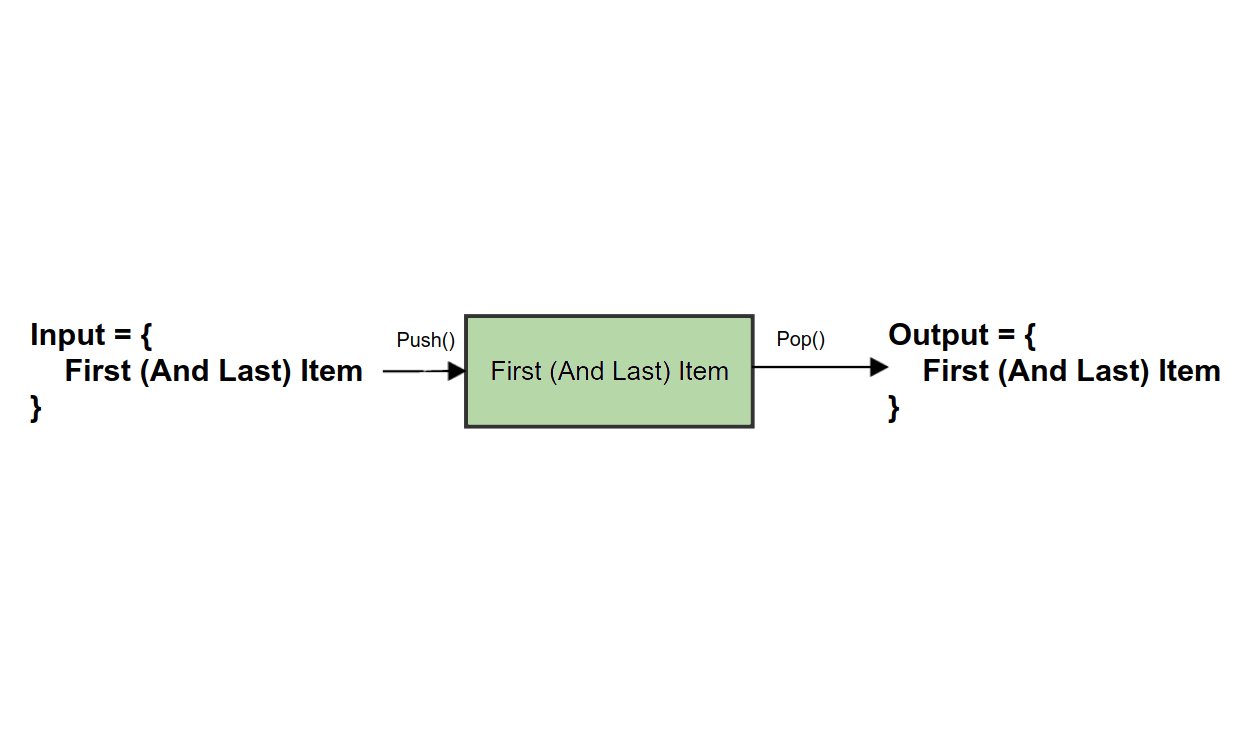 |
For whatever reason, this corner case causes my brain power utilization to spike to 100% for a few seconds (probably an n^2 code path somewhere) every time someone mentions the phrase 'FIFO' or 'LIFO'. It's quite awful actually since it causes extreme lag every time I try to have a conversation with someone about data structures or algorithms.
Now I know that some of you out there aren't going to agree with me in saying that the use of 'FIFO' and 'LIFO' is a problem, but from a pedagogical perspective, I think it's worth discussing because at some point you have to learn these terms for the first time and we might as well be teaching these things as efficiently as possible. Furthermore, if we're going to repeat this thousands of times in textbooks and literature everywhere, why not make it as clear as possible?
The First/Last of What Exactly?
The terms 'FIFO' and 'LIFO' make reference to a 'first one' and a 'last one'. But an important question is 'first/last one among what set of elements?' The only reasonable choices are the following:
- 1) The first/last one among the set of items that you are about to add to the data structure.
- 2) The first/last one among the set of items that you are about to add to the data structure, unioned with the set of items that are already in the data structure.
Since data structures are typically considered 'black boxes' that simply do stuff for us without disclosing their inner details, it is tempting to consider using interpretation #1 from the above choices when interpreting the definition of 'FIFO' and 'LIFO'. This interpretation always works for stacks, but it only works for queues if they are initially empty! The interpretation #2 always works for both, but requires the reader to consider the possibly unknown internal state of the data structure. If you first put the number 3 into a queue, then put the number 5 into a queue, then remove an item from the queue, what will be the first thing out of the queue? Nobody knows! It might be the first thing you put in, but it also might be the first thing that someone else put in! It could be anything!
FIFO, FOFI, LIFO, FOLI, FILO and LOFI
The interchangeability of 'First' vs. 'Last' and 'Input' vs. 'Output' also opens the door for us to question whether there are also other 'easy to remember' acronyms that can come out of the following regex:
[FL][IO][FL][IO]
For example, assigning F=0, L=1, I=0, O=1:
| #### | Acronym | Phrase | Explanation |
| 0000 | FIFI | 'First In First In' | A tautology. |
| 0001 | FIFO | 'First In First Out' | The familiar definition above used for queues. |
| 0010 | FILI | 'First In Last In' | Not a particularly meaningful data structure, but could be used to describe a single variable's behaviour. |
| 0011 | FILO | 'First In Last Out' | This is equivalent to the term 'LIFO' for describing stacks, and it is found in literature, but much less frequently. Often this is the acronym that my mind comes up with when searching for the acronym for stack behaviour. Unfortunately, because of its infrequent use it leads to confusion. |
| 0100 | FOFI | 'First Out First In' | A re-arrangement of FIFO, but no one uses this acronym. You could be the first; start a revolution! |
| 0101 | FOFO | 'First Out First Out' | A tautology. |
| 0110 | FOLI | 'First Out Last In' | A re-arrangement of LIFO, but no one uses this acronym. |
| 0111 | FOLO | 'First Out Last Out' | This one would seem similar to FILI, but I think that you might be able to make a meaningful use of this acronym for primarily write-only buffers where you can 'unput' only a single character. You might also be able to make a meaningful connection to LR(1) or LL(1) parsers too. |
| 1000 | LIFI | 'Last In First In' | A re-arrangement of FILI. |
| 1001 | LIFO | 'Last In First Out' | Our familiar acronym for describing stacks. |
| 1010 | LILI | 'Last In Last In' | A tautology. |
| 1011 | LILO | 'Last In Last Out' | A less frequently used acronym used to describe the behaviour of queues. |
| 1100 | LOFI | 'Last Out First In' | A re-arrangement of the infrequently used FILO. |
| 1101 | LOFO | 'Last Out First Out' | A re-arrangement of FOLO. |
| 1110 | LOLI | 'Last Out Last In' | A re-arrangement of LILO. |
| 1111 | LOLO | 'Last Out Last Out' | A tautology. |
| 2111 | YOLO | 'Yolo, California' | An unincorporated community in California. |
As a summary of the above table:
- The following acronyms from the above list correctly describe the behaviour of queues: FIFO, FOFI, LILO, LOLI.
- The following acronyms from the above list correctly describe the behaviour of stacks: LIFO, FOLI, FILO, LOFI.
An Alternative Definition
I hereby decree, with universal authority, that the terms 'FIFO' and 'LIFO' shall no longer be used.
It is therefore mandated that the following alternative terms be implemented in their place effective immediately:
- SSOU - Subsequence Order Unchanging
- STOR - Substring Order Reversing
Furthermore,
- Queues are SSOU.
- Stacks are STOR.
Queues are Sue and stacks are store.
An Input/Output History shall be defined as an ordered sequence of statements H = {IO_0, IO_1, IO_2, ..., IO_N} that describe what data was input, and output from a data structure over the course of its lifetime. Furthermore, the ordering of each IO statement in the IO history is arranged such that IO_n is guaranteed to have occurred before IO_n+1 for all n < N. IO statements are assumed to never occur at the same instant in time. An Input/Output History shall consider all IO operations from the instant the data structure was created until it was destroyed. Furthermore, it is considered true that the data structure begins and ends its life empty.
A data structure is SSOU, if for any input/output history, q = {IO_0, IO_1, IO_2, ..., IO_N}, it is true that for any subsequence of input items i = {I_A, I_B,...I_M}, there exists a corresponding subsequence of output items o = {O_T, O_U,...O_Z}, where I_A = O_T, I_B = O_U, ..., I_M = O_Z, and furthermore, the partial order of items in i is identical to the partial order of items in o.
A data structure is STOR, if for any input/output history, s = {IO_0, IO_1, IO_2, ..., IO_N}, it is true that for any substring of input items I_A, I_A+1, I_A+2,...I_A+k, there exists a corresponding subsequence of output items O_B, O_C, O_D,...O_E, where the partial order of the output items is the reverse of the partial order of the input substring, and I_A = O_B, I_A+1 = O_C, I_A+2 = O_D, ..., I_A+k = O_E.
The pronunciation of 'SSOU' is the same as the name 'Sue' is (it rhymes with queue). The pronunciation of 'STOR' sounds exactly like the pronunciation of the word 'store'. The spoken language to be used when interpreting these pronunciations is Canadian English as spoken in the province of Ontario in the year 2017. All other pronunciations are strictly prohibited.
The above definitions must appear in the exact form above, and any alteration is strictly prohibited.
Substring VS. Subsequence
Please note: If you mix up the definition of substring with subsequence you're going to have a bad time. Pay special attention to the difference between these words in this article.
A Visual Explanation
| For stacks, the order of any input substring will appear as an output subsequence will reversed order. | For queues, the order of any input subsequence will appear unchanged as an output subsequence. |
Is This Definition Actually Better?
I claim that it is, primarily because it is less ambiguous about what operations are performed on your data. This is contrasted with the concept of 'first' and 'last' in the conventional definition because of the question mentioned earlier: "First or last among the items being inserted, or all items?"
It is also better because it focuses on the operation being performed on the data, which is mutually exclusive for stacks vs. queues, instead of the properties of the output which are not mutually exclusive when n = 1. Furthermore, the inclusion of the word 'ordering' forces the reader to visualize a sequence of items when attempting to understanding the behaviour of a base case instead of potentially considering the edge case with one item where both properties apply.
You might argue that it is still correct to say the output is 'reversed' in the queue when n = 1 because the results are the same, but it would be just as convincing to argue the other way as a matter of semantics. In the case of FIFO, LIFO, you must unequivocally admit that when there is only one item, it is both the first and the last item.
Conclusion
As we've seen above, there are a number of confusing aspects to the terms 'FIFO' and 'LIFO'. These confusing aspects stem from the lack of a formal definition for queues and stacks, but also from the ease with which you can create variations of the input/output, first/last acronyms.
Therefore, if you've recently commissioned a textbook printing to use the phrases 'FIFO' or 'LIFO', please consider burning them (at your own expense) and have them re-printed to use the above superior terminology.
 The Regular Expression Visualizer, Simulator & Cross-Compiler Tool
Published 2020-07-09 |
 Buy Now -> |
 Why Is It so Hard to Detect Keyup Event on Linux?
Published 2019-01-10 |
 Myers Diff Algorithm - Code & Interactive Visualization
Published 2017-06-07 |
 Interfaces - The Most Important Software Engineering Concept
Published 2016-02-01 |
 Regular Expression Character Escaping
Published 2020-11-20 |
 How Do Regular Expression Quantifier Work?
Published 2020-08-18 |
 Overlap Add, Overlap Save Visual Explanation
Published 2018-02-10 |
| Join My Mailing List Privacy Policy |
Why Bother Subscribing?
|