Overlap Add, Overlap Save Visual Explanation

2018-02-10 - By Robert Elder

This article is effectively an appendix to the article The Fast Meme Transform: Convert Audio Into Linux Commands. In this article, we will review the 'Overlap Add' and 'Overlap Save' algorithms which can be used to accomplish several intimately related mathematical tasks:

Correctly re-constructing a longer time-domain signal from Fourier coefficients of smaller intervals of that signal.
Correctly performing filtering in the frequency domain.
Applying a digital filter to an infinite length signal.
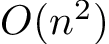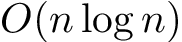Reducing the asymptotic runtime of a discrete convolution from $O(n^2)$ to $O(n\log{}n)$ by transforming the convolution into a discrete Fourier transform.
Fast multiplication of numbers.

For some added context on the problem being solved here, our task is to find the discrete convolution of x[n] and h[n]. x[n] represents a discrete sequence of samples of our time domain signal. h[n] represents the time domain sequence of the digital filter we wish to apply. While x[n] represents the signal in the time domain, X[n] denotes a sequence of the same length as x[n], but in the frequency domain. Similarly, H[n] represents the filter in the frequency domain. Transforming x[n] into X[n] or X[n] into x[n] is accomplished by using the Discrete Fourier Transform.

The variable M represents the length of the filter sequence. The variable 'L' is the number of samples in each interval that our longer signal will be broken up into. A common question is "How do you determine the value of L?" and the answer, in general, is that you can choose any value of L that you want. However, L is often chosen so that the sum of L + M -1 is a power of two because this is a requirement of the much faster Fast Fourier Transform algorithm. Of course, you can always just use the slower Fourier Transform algorithm and get the same result for any sequence length.

An example of the higher-level goal of this operation would be something like increasing or decreasing certain frequencies in a piece of music as is done in an audio equalizer. Another example would be for removing noise from a radio signal.

The example calculations below will update dynamically based on any changes you make to the inputs:

Signal x[n] (time domain):

Filter h[n] (time domain):

L =

M = len(h[x]) =

N = L + M - 1 =

Convolution By Overlap Add

Below, you will see the partitioning step of the overlap add algorithm:

Now that the signal has been partitioned into intervals labeled x_i[n], there are two methods that could be used to calculate the convolution between the signal and the filter, both of which are mathematically correct. These methods are the Fourier transform method, and the trivial multiply and add calculation which can be expressed as a matrix multiplication. For more details on the matrix calculation for performing convolution, see Toeplitz Matrix.

Now that the contribution of each interval has been calculated as y_i[n], we can add them together to determine the full final filtered time-domain signal y[n]:

As you can see above, the result y[n] is the result of performing the convolution between the signal x[n] and the filter h[n]. This concludes the example calculation using the overlap add method, with y[n] as our final answer.

Convolution By Overlap Save

In the overlap save algorithm, the first M-1 elements of the current x_i[n] interval are 'saved' from the overlap last of the previous x_(i-1)[n] interval. This is where the name 'overlap save' comes from. The initial 'saved' values are simply set to zero.

The calculation step is quite similar to that found in the overlap add algorithm. One notable difference from the overlap add method is in overlap add, the zero padding that occurs on the end of each x_i[n] interval ensures that the circular convolution is equivalent to the linear convolution. This means that with overlap add, the matrix calculation need not actually have non-zero elements in the upper right-hand corner of the filter matrix since they will always be multiplied against zero elements. However, in overlap save this is not the case, and circular convolution must be used.

Below, you will observe that the red 'overlap' elements are 'scraped' or set to zero. This is where the alternate name 'overlap scrap' comes from. With overlap save there is no 'adding' of overlapping output intervals as there was with overlap add.

As you can see above, the result y[n] is result of performing the convolution between the signal x[n] and the filter h[n]. This concludes the example calculation using the overlap save method.

What's The Difference Between Overlap Add And Overlap Save?

Here is a simple summary of differences between overlap add and overlap save that might influence which one you use:

Overlap add will involve adding a number of values in the output to recover the final signal, whereas overlap save does not require any addition in this step. This might be important to you if you want to consider the numerical precision of your output, or if you want to reduce the number of addition operations.
The Overlap add method can be computed using linear convolution since the zero padding makes the circular convolution equal to linear convolution in these cases.
The Overlap save method doesn't do as much zero padding, but instead re-uses values from the previous input interval. In overlap save, some values are considered contaminated due to aliasing of the circular convolution, so they are discarded from the output.
In overlap save there is less zero padding. In fact, the only time you need to zero pad is before the first interval, and after the last interval if the length of the input sequence isn't evenly divided by L.

Extra Notes About This Article

Since the definition of the Fourier transform is not well standardized, you may be wondering which version was used in the calculations above (if you want to compare your numbers). The forward discrete Fourier transform used in this article (denoted as DFT) was:

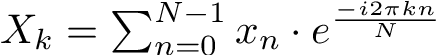
$X_k = \sum_{n=0}^{N-1} x_n \cdot e^{\frac{-i2{\pi}kn}{N}}$

And the reverse discrete Fourier transform used in this article (denoted as IDFT) was:

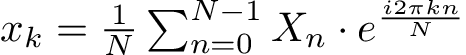
$x_k = \frac{1}{N} \sum_{n=0}^{N-1} X_n \cdot e^{\frac{i2{\pi}kn}{N}}$

You can check out Wikipedia for a more detailed explanation of the variables in the above formula.

With regards to accuracy, it should be noted that in some cases the results from the Fourier transform method above don't always exactly match those found by the matrix multiplication method. This is because of floating point errors that occur, mainly in the sin and cos functions. The numbers displayed in this article are rounded, so they mostly end up being the same but you'll occasionally see small differences.

Finally, I should note that the details included in this article are at the limits of my knowledge on this subject. If you believe you have found an error above, please let me know so I can correct it at info@robertelder.org.

Using Fourier Transforms To Multiply Numbers - Interactive Examples Published 2019-01-10	$35.00 CAD Alan Turning, Ada Lovelace, Kurt Gödel Portaits	Endpoint Discontinuities and Spectral Leakage Published 2018-02-10	Fourier Transform Coefficients Of Real Valued Audio Signals Published 2018-02-10
The Regular Expression Visualizer, Simulator & Cross-Compiler Tool Published 2020-07-09	Why Is It so Hard to Detect Keyup Event on Linux? Published 2019-01-10	Myers Diff Algorithm - Code & Interactive Visualization Published 2017-06-07	Interfaces - The Most Important Software Engineering Concept Published 2016-02-01

Why Bother Subscribing?

Free Software/Engineering Content. I publish all of my educational content publicly for free so everybody can make use of it. Why bother signing up for a paid 'course', when you can just sign up for this email list?
Read about cool new products that I'm building. How do I make money? Glad you asked! You'll get some emails with examples of things that I sell. You might even get some business ideas of your own :)
People actually like this email list. I know that sounds crazy, because who actually subscribes to email lists these days, right? Well, some do, and if you end up not liking it, I give you permission to unsubscribe and mark it as spam.